How to make sense of Model Checking
I’ve recently started to explore the ideas behind model checking. This post documents my findings through a Q&A format, in hopes of making it easier to follow especially for those who are not familiar with the subject. I start off with basics – what it does and what it is for, illustrating the mechanism with simple examples – and answer any questions that came to my mind while thinking it through.
Q1: What is model checking?
A: When you are designing a program, you want your program to correctly behave based on your implementation design. As the software systems have grown bigger and highly complex, we can no longer rely on manual reasoning to verify programs. Instead, we make use of a more automated mechanism – i.e., model checking – to analyze correct behavior of complex programs.
That is, model checking is an automated technique that, given a finite-state model of a system and a formal property, exhaustively and systematically checks whether the model satisfies this property, behaving just as the specifications of the property instructed it to. The main goal of model checking is to prove properties of program computations.1 In this process, model checkers employ different kinds of algorithms (e.g., partial order reduction, bit-state hashing1) to make the verification runs more effective.
Q2: What are the steps involved in model checking?
A: The model checking process consists of three different phases: modeling, running, and analysis phase2.
- In the modeling phase, we model the system using the modelling language to express it as finite-state systems and formalize the property using the property specification language.
- The system under consideration is compiled into a state-transition graph (a.k.a. Kripke structure, as shown in Fig 1.3 below) K, the specification is expressed as a temporal-logic formula φ, and the model checker decides whether K ⊨ φ, i.e., whether a structure K is a model of the formula φ.
- We may run some simulations of the model as a sanity check during the modeling phase.
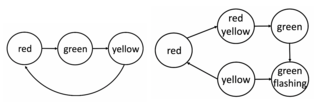
Fig 1. American and Austrian traffic lights as Kripke structure - In the running phase, we run the model checker to assess whether the property holds for a given state in the model.
- Once the model checker is run, there are three possible outcomes in the analysis phase: property being satisfied, violated, or insufficient memory triggering out-of-memory error.
- If property is satisfied, then check the next property (if any).
- If it is violated analyze the counterexample generated by the model checker, refine the model or property, and repeat the entire process.
- If you run out of memory, reduce the size of the model and try it again.
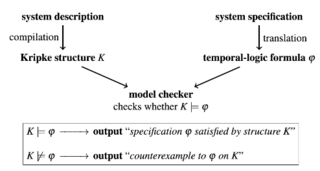
Fig 2. Basic model-checking methodology
Q3: What are some examples of the model checking tools?
A: There are quite a few open-source model checkers. They differ by the modelling language (C, Promela, etc.), properties language (LTL, CTL, etc.), performance in verifying properties of different systems, etc. Examples of the model checking tools include SPIN, NuSMV, UPPAAL, PRISM, PAT, and TLC, among many others.
Q4: What are some examples of programs verified by a model checker?
A: Let’s first look at the following examples where we use the SPIN model checker, one of the most popular open-source model checking tools used for concurrent and distributed systems. The model is designed in Promela (short for Process Meta Language) language.
Example 1. Verifying non-termination of a traffic light controller4
Suppose we have a traffic light controller system where light switches from green to yellow, then to red, and so on, as shown below:
mtype = {red, yellow, green};
mtype color = green;
active proctype TrafficLightController() {
do
::(color == red) -> color = green;
::(color == yellow) -> color = red;
::(color == green) -> color = yellow;
od;
}
Once we run SPIN, it results in ‘unreached in proctype’ message as follows:
unreached in proctype TrafficLightController
trafficlight.pml:16, state 13, "-end-"
(1 of 13 states)
This indicates that the proctype never reaches the “end” state, which is what we expected as there is a non-terminating loop in the program.
Example 2. Verifying that traffic lights are never green simultaneously5
Now, let’s say we have the following system of two traffic lights and a controller, and want to verify the safety property that the two lights are never green simultaneously:
bit g1=0, g2=0;
active proctype TrafficLights()
{
do
:: atomic{ (g1==0 && g2==0) -> g1=1; g2=0 }
:: atomic{ (g1==0 && g2==0) -> g1=0; g2=1 }
:: atomic{ (g1==1 && g2==0) -> g1=0; g2=0 }
:: atomic{ (g1==0 && g2==1) -> g1=0; g2=0 }
od;
}
ltl P1 {[] (! (g1 && g2))}
Running SPIN results in the following outcome:
$ spin -a lights_simple.pml
$ gcc -o pan pan.c
$ ./pan -a -n P1 lights_simple.pml
(Spin Version 6.5.1 -- 6 June 2020)
+ Partial Order Reduction
Full statespace search for:
never claim + (P1)
assertion violations + (if within scope of claim)
acceptance cycles + (fairness disabled)
invalid end states - (disabled by never claim)
State-vector 28 byte, depth reached 3, errors: 0
3 states, stored
2 states, matched
5 transitions (= stored+matched)
0 atomic steps
hash conflicts: 0 (resolved)
Note that I have first generated a verifiable source code in pan.c, and then compiled and executed the verifier.
Example 3. Verifying a mutual exclusion algorithm6 7
Suppose we have the following model based on Peterson’s algorithm for mutual exclusion:
bool turn; // indicates whose turn to enter the CS
bool flag[2]; // indicates if a process is ready to enter the CS
active [2] proctype user()
{
again:
flag[_pid] = true; // _pid: identifier of the process
turn = _pid;
(flag[1-_pid] == false || turn == 1-_pid);
/* critical section */
flag[_pid] = false;
goto again:
}
We are interested in verifying safety properties that there are only at most two instances with identifiers 0 and 1, and that there is always at most one process entering the critical section. These properties can be verified by adding the assertions and specifying an LTL formula as follows:
bool turn, flag[2];
byte ncrit; // counts the number of processes in critical section
active [2] proctype user()
{
assert(_pid == 0 || _pid == 1);
again:
flag[_pid] = true;
turn = _pid;
(flag[1-_pid] == false || turn == 1-_pid);
ncrit++;
assert(ncrit == 1); /* critical section */
ncrit--;
flag[_pid] = false;
goto again:
}
ltl P1 { [] (ncrit <= 1) }
Running the SPIN results in the following outcome:
$ spin -a peterson.pml
$ gcc -o pan pan.c
$ ./pan -a -n P1 peterson.pml
(Spin Version 6.5.1 -- 6 June 2020)
+ Partial Order Reduction
Full statespace search for:
never claim + (P1)
assertion violations + (if within scope of claim)
acceptance cycles + (fairness disabled)
invalid end states - (disabled by never claim)
State-vector 36 byte, depth reached 49, errors: 0
40 states, stored
27 states, matched
67 transitions (= stored+matched)
0 atomic steps
hash conflicts: 0 (resolved)
Q5: What are some examples of these properties? How can you classify them?
A: With the SPIN model checker, we can check deadlocks (as in invalid endstates), correctness of system invariants via user-inserted assertions, unreachable code, LTL formula, and liveness properties through non-progress cycles (livelocks) or acceptance cycles8.
The properties can be classified into two categories: safety and liveness. Informally speaking, safety properties stipulate that “bad things” do not happen during program computations, whereas liveness properties stipulate that “good things” will eventually happen1. Safety properties are verified via invariants such as “x is always less than 5”, or deadlock freedom such as “the system never reaches a state where no actions are possible”. Specifically, SPIN can find a trace leading to the “bad” thing. If there is no such trace, we know that the property holds. On the other hand, liveness properties are verified via termination that “the system will eventually terminate” or response that “if action X occurs then eventually action Y will occur”. SPIN can search for a loop in which the good thing does not happen. If there is no such loop, then we know that the property is satisfied.
Q6: How do we formalize requirements into property specifications?
A: The requirements are formalized into property specifications via propositional temporal logic, so that we have precise and unambiguous formulation of properties under consideration. As for the SPIN model checker, for example, linear temporal logic (LTL) formulae are used to specify requirements. LTL is a mathematical language for describing linear-time propositions, and its formulae consist of propositional logic and temporal logic operators.
Primary operators are:
- <> (“eventually”): a property will become true at some point in the future, and
- [] (“always”): a property is satisfied now and forever into the future.
For example, the property that the two lights are never green simultaneously, i.e., [] (! (g1 && g2)), from the Example 2 above can be expressed in LTL as ▢ ¬(g1∧g2).
Some of the common composite operators include:
- p -> ♢ q p implies eventually q (response)
- p -> q U r p implies q until r (precedence)
- ▢♢p always eventually p (progress)
- ♢▢p eventually always p (stability)
- ♢p -> ♢q eventually p implies eventually q (correlation)
More details can be found in the reference source5.
Q7: What are pros and cons of model checking compared to other comparable techniques?
A: Other related approaches are testing, abstract interpretation (and other program analyses), and higher-order theorem proving. Comparison of the techniques can be summarized as follows3:
| Testing | Model Checking | Abstract Interpretation | Theorem Proving |
|---|---|---|---|
| + Fastest and simplest way to detect error | + Systematic approach to automatic bug detection aimed at model verification | + Similar to model checking, employs algorithms to prove properties automatically | Compared to model checking, focus is on expressiveness rather than efficiency |
| + Relatively easy to automate | + Applicable at different stages of design process | Built on lattice theory rather than logic | - Typically incorporates manual work, especially for complex systems |
| - “Program testing can be used to show the presence of bugs, but is hopelessly inadequate for showing their absence” | + Well-suited for finding concurrency bugs and proving their absence | Compared to model checking, focus is on efficiency rather than expressiveness, on code rather than models | - Time-consuming and often non-trivial task worthy of a research publication |
Q8: What is the trend in model checking research?
A: The handbook of model checking3 classifies advances in model checking into two recurrent themes, driving much of the research agenda: the algorithmic challenge and the modelling challenge.
- The algorithmic challenge refers to the problem of designing model-checking algorithms that scale to real-life problems. This is due to the so-called “state-explosion problem”, the combinatorial explosion of states in the Kripke structure. Because state space is not finite in most situations (e.g., unbounded memory, unbounded number of parallel processes), this leads to the modelling challenge.
- The modelling challenge refers to the problem of extending the model-checking framework beyond Kripke structures and temporal logic. We need to extend modelling and specification frameworks to model and specify unbounded iteration and recursion, unbounded concurrency and distribution, unbounded data types, real-time and cyber-physical systems, probabilistic computation, etc. Some extensions maintain decidability, while others sacrifice decidability and maintain the ability to find bugs automatically, systematically, and early in the system design process.
In addition, there has been a recent development in convergence between model checking and other related approaches such as white-box testing techniques, abstract interpretation, and theorem proving.
References
-
Jhala, Ranjit, and Rupak Majumdar. “Software Model Checking.” ACM Computing Surveys 41, no. 4 (2009): 1–54. https://doi.org/10.1145/1592434.1592438. ↩ ↩2 ↩3
-
Baier, Christel, Joost-Pieter Katoen, and Kim Guldstrand Larsen. “System Verification.” In Principles of Model Checking, 1–18. Cambridge, MA: MIT Press, 2014. ↩
-
Clarke, Edmund M., Thomas A. Henzinger, and Helmut Veith. “Introduction to Model Checking.” In Handbook of Model Checking, 1–22. Springer Publishing Company, 2018. ↩ ↩2 ↩3
-
Roychoudhury, Abhik. “Automated Software Validation.” CS5219 Week 6 Resources. Accessed July 18, 2020. https://www.comp.nus.edu.sg/~abhik/5219/old-lesson-plan.html. ↩
-
Murray, Richard M., Nok Wongpiromsarn, and Ufuk Topcu. “Computer Lab 1: Model Checking and Logic Synthesis using Spin.” Class lecture, Specification, Design, and Verification of Networked Control Systems from California Institute of Technology, Pasadena, CA, March 19, 2013. ↩ ↩2
-
Chechik, Marsha. “Partial order reduction and Promela/SPIN.” Class lecture, Automated Verification from University of Toronto, Toronto, ON, 2007. ↩
-
“Spin Verification Examples and Exercises.” Spin - Formal Verification, November 28, 2004. http://spinroot.com/spin/Man/Exercises.html. ↩
-
Ben-Ari, Mordechai. “Verification with Temporal Logic.” In Principles of the Spin Model Checker, 68–93. London: Springer, 2008. ↩